算法初级和数据结构
结构化编程
- 一行一行执行
- 有条件控制语句 if…else…
- 有循环控制语句 while(exp) do…
伪代码的好处
- 不用纠结于语法的细节,因为语法是你自己定的
- 可以体会语言设计者的想法,因为语法是你自己定的
什么是算法
以下是高德纳在他的著作《计算机程序设计艺术》里对算法的特征归纳:1
2
3
4
5输入:一个算法必须有零个或以上输入量。
输出:一个算法应有一个或以上输出量,输出量是算法计算的结果。
明确性:算法的描述必须无歧义,以保证算法的实际执行结果是精确地匹配要求或期望,通常要求实际运行结果是确定的。
有限性:依据图灵的定义,一个算法是能够被任何图灵完备系统模拟的一串运算,而图灵机只有有限个状态、有限个输入符号和有限个转移函数(指令)。而一些定义更规定算法必须在有限个步骤内完成任务
有效性:又称可行性。能够实现,算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现。
什么是数据结构
数据结构就是数据的结构
一般来说是这样的:
- 我们要解决一个跟数据相关的问题
- 分析这个问题,想出对应的数据结构
- 分析数据结构,想出算法
数据结构和算法是互相依存、不可分开的
你学习完排序算法,就能了解常见的数据结构
大分类
- 分治法:把一个问题分区成互相独立的多个部分分别求解的思路。这种求解思路带来的好处之一是便于进行并行计算。
- 动态规划法:当问题的整体最优解就是由局部最优解组成的时候,经常采用的一种方法。
- 贪婪算法:常见的近似求解思路。当问题的整体最优解不是(或无法证明是)由局部最优解组成,且对解的最优性没有要求的时候,可以采用的一种方法。
- 线性规划法:见词条。
- 简并法:把一个问题通过逻辑或数学推理,简化成与之等价或者近似的、相对简单的模型,进而求解的方法。
我们前端主要使用分治法——分而治之。
排序算法
冒泡排序
时间复杂度每次比较两个相邻的数字作比较,小数放前面,大数放后面,这样一轮下来小的数字就拍在了最前面,如此重复,直到所有的数字排完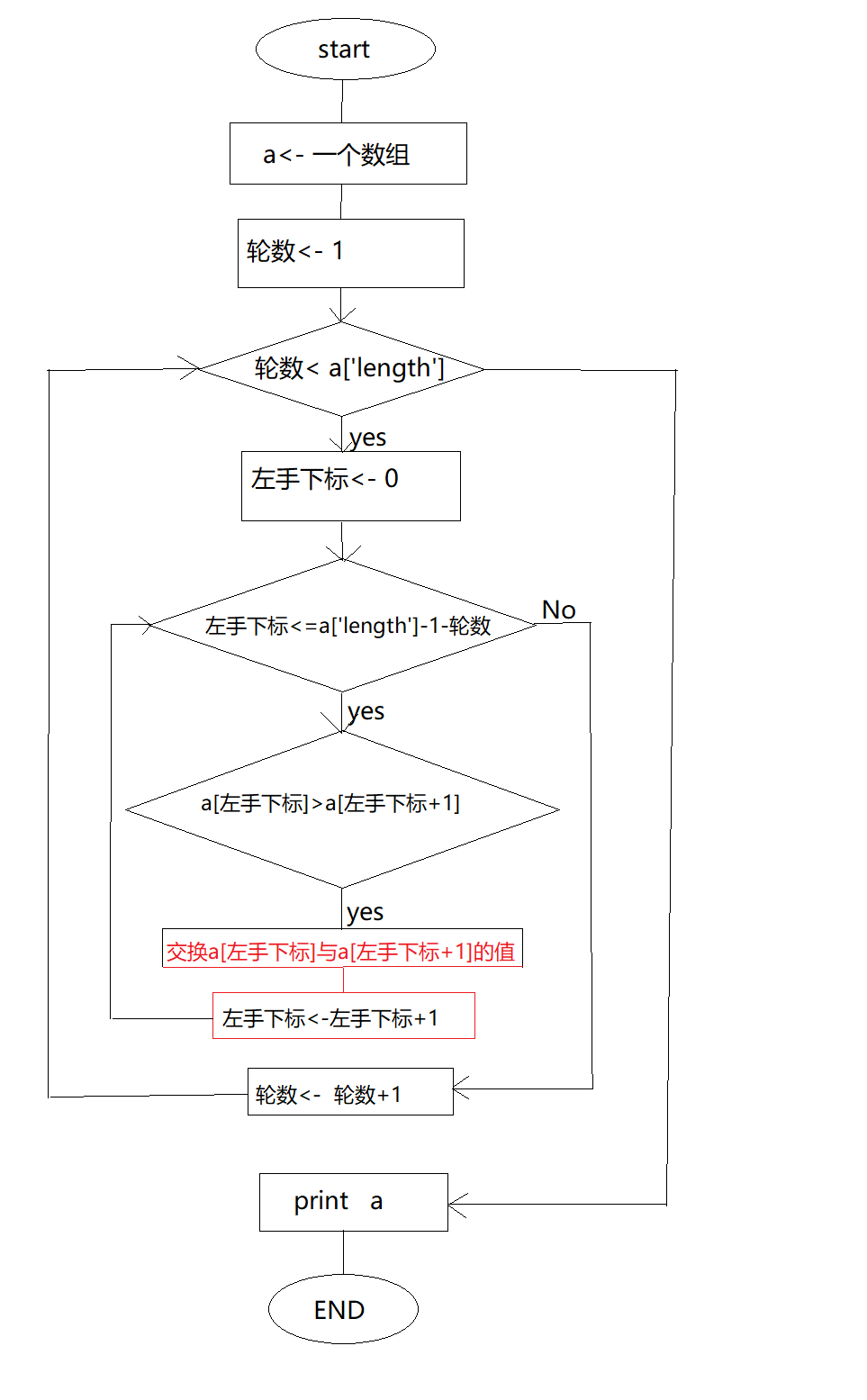
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17var babelSort = function(array) {
//tem = 用于交换数组的辅助参数
var tem
var a = array
//i = 轮数
for(var i = 1; i < a.length; i++) {
//j = 下标
for(var j = 0; j < a.length - 1;j++) {
if (a[j] > a[j + 1]) {
tem = a[j]
a[j] = a[j + 1]
a[j + 1] = tem
}
}
}
return array
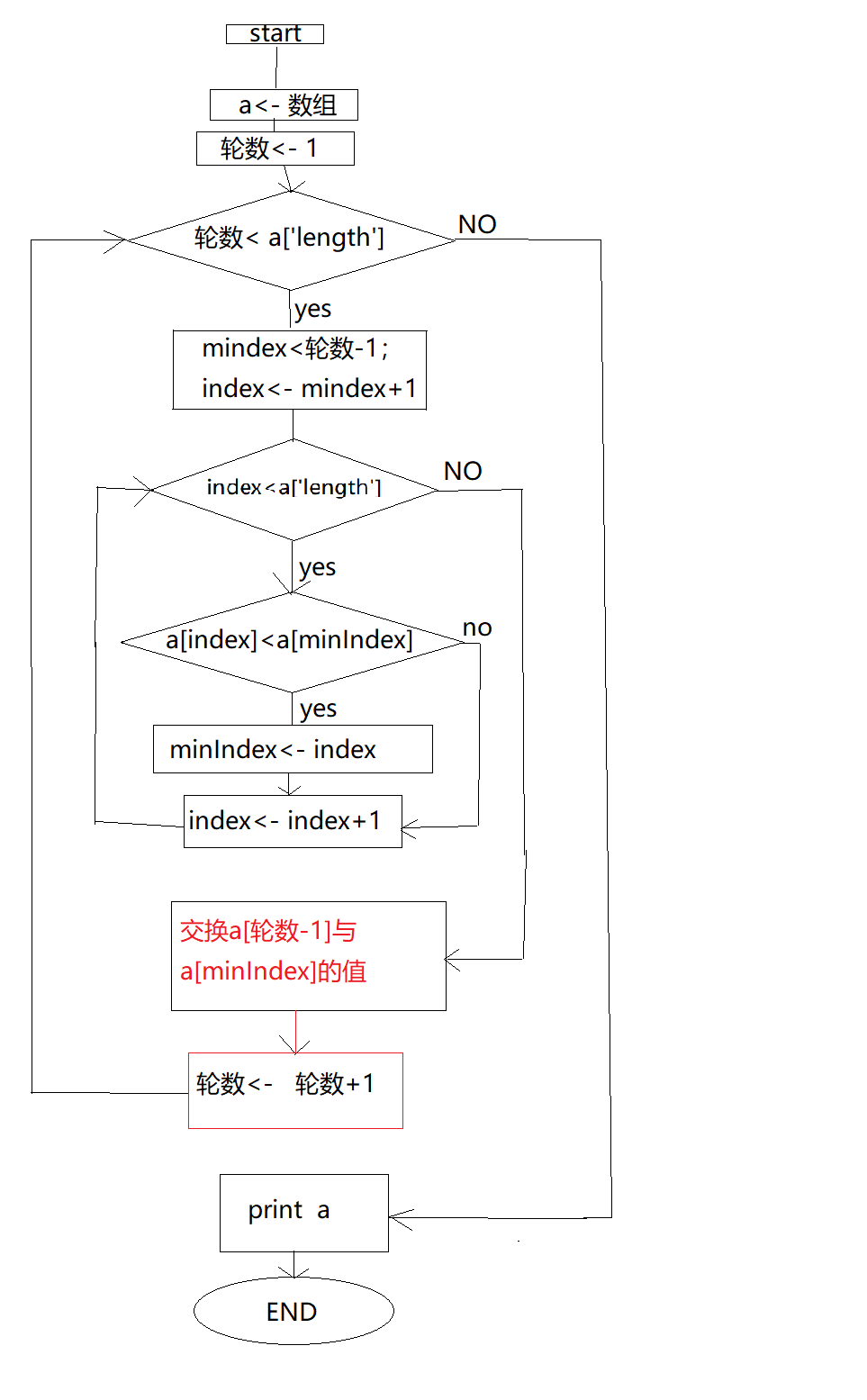
}选择排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15var selectSort = function(array){
var a = array
//j = 下标
for(var j = 0; j < a.length - 1; j++){
//jump = 跳跃数
for(var jump = 1; jump < a.length; jump++) {
if (a[j] > a[j + jump]){
var tem = a[j]
a[j] = a[j + jump]
a[j + jump] = tem
}
}
}
return array
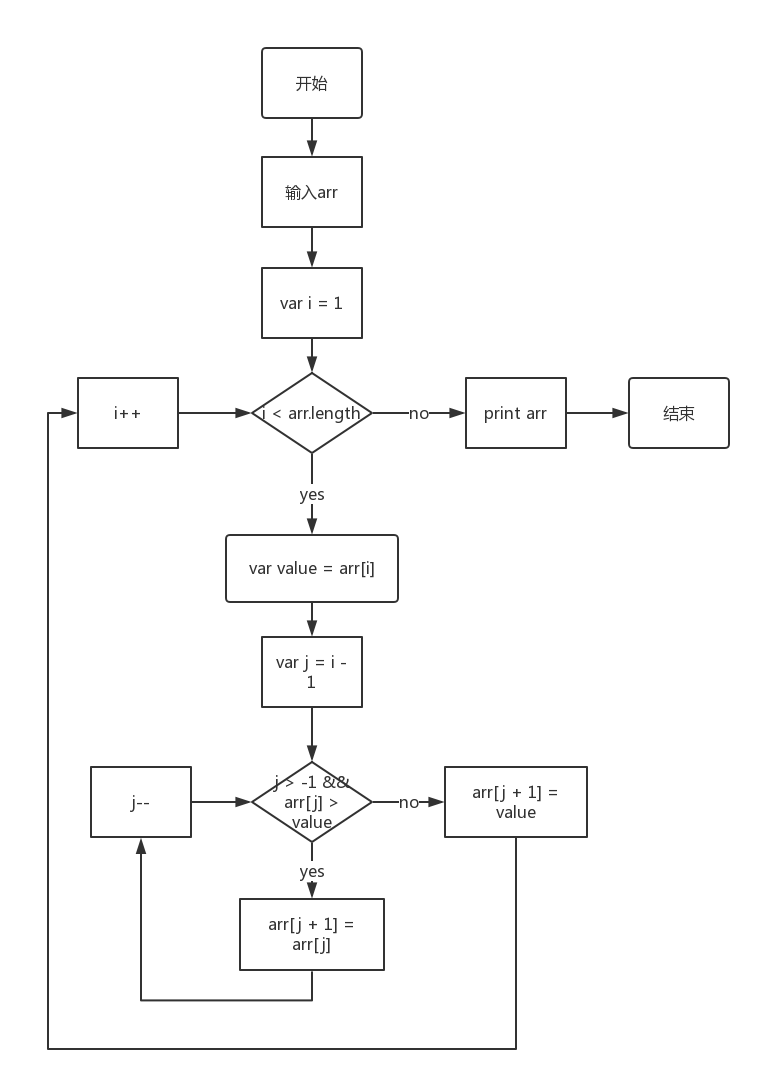
}插入排序
1
2
3
4
5
6
7
8
9
10var insertSort = function(array){
for(var i = 1; i < array.length; i++){
var value = array[i]
for(var j = i - 1; j > -1 && array[j] > value; j--){
array[j + 1] = array[j]
}
array[j + 1] = value
}
return array
}基数排序
时间复杂度O(n + max) 所有正整数总从最低的以为开始,把相同最低位相同的排列在一起,然后在排十位,不够的补零,然后在依次在排下一位,这样排列下来,在挨个去取即可得到有序数列了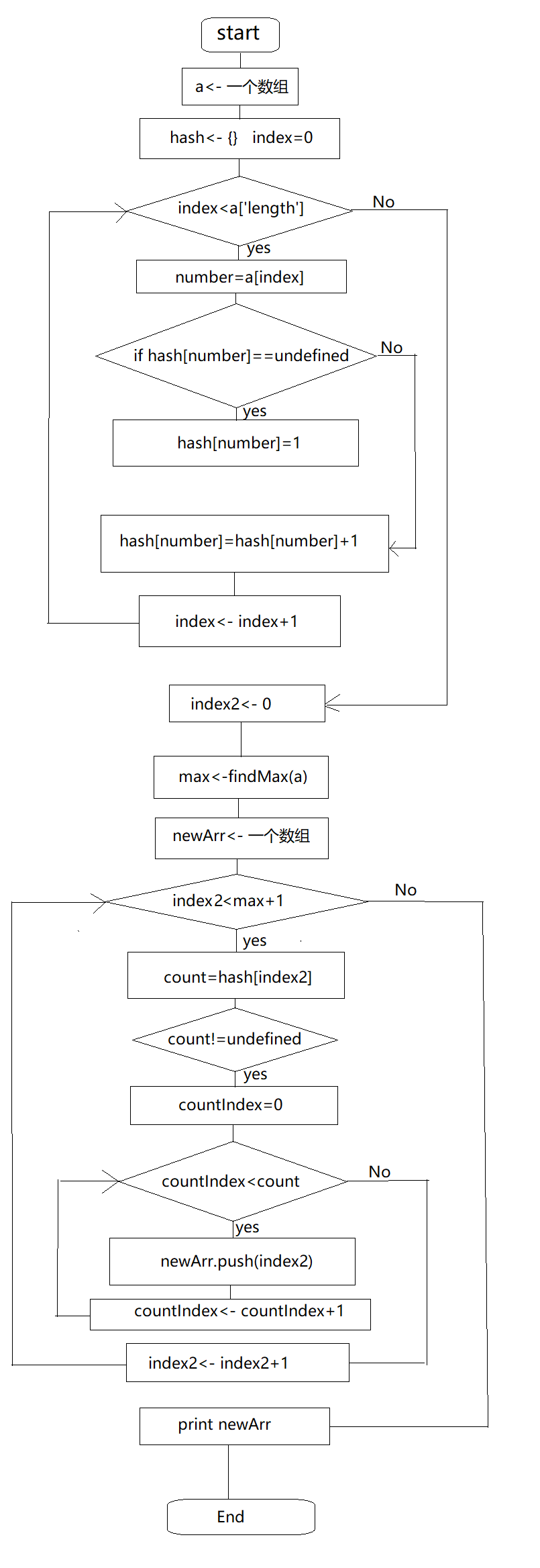
- 快排
时间复杂度O(n log2 n) 找其中的一个数作为标杆,小于标杆的数字放在左边,大于标杆的数字放在右边,这一次排完之后再重复前面的操作,直到只有一个数字为止 - 归并排序
- 堆排序:将数组作为一个完全二叉树的顺序存储,将这个二叉树调整为最大堆,取出根节点元素后将最后一个节点换至堆顶,然后循环调整二叉树为最大堆,取出根节点的操作。
- 计数排序
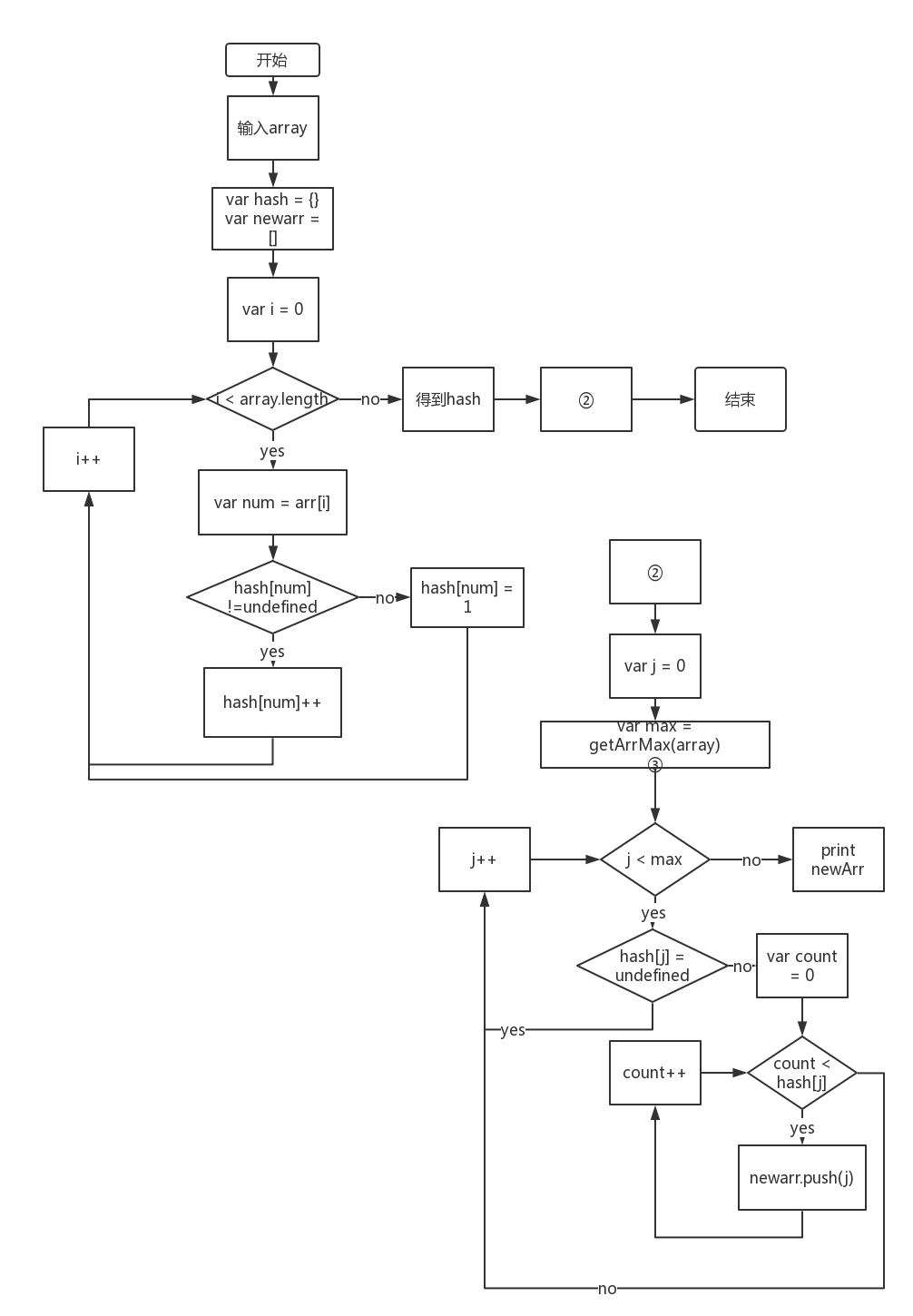
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32var countSort = function(array) {
var hash = {}
var newarr = []
for(var i = 0; i < array.length; i++){
var num = array[i]
if (hash[num] != undefined){
hash[num] ++
} else {
hash[num] = 1
}
}
var max = getArrMax(array)
for(var j = 0; j < max; j++){
if (hash[j] == undefined){
//什么也不做
} else {
for(var count = 0; count < hash[j]; count++){
newarr.push(j)
}
}
}
return newarr
}
var getArrMax = function(array){
var max = array[0]
for (var i = 1; i < array.length; i++){
if (array[i] > max){
max = array[i]
}
}
return max
}
9.桶排序1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68function bucketSort(array, step) {
var result = [],
bucket = [],
bucketCount,
l = array.length,
i,
j,
k,
s,
max = array[0],
min = array[0],
temp;
i = 1
while(i < l){
if (array[i] > max) {
max = array[i]
}
if (array[i] < min) {
min = array[i];
}
i++
}
min = min - 1;
bucketCount = Math.ceil((max - min) / step); // 需要桶的数量
i = 1
while(i < l){
temp = array[i];
j = 0
while(j < bucketCount){
if (temp > (min + step * j) && temp <= (min + step * (j + 1))) { // 判断放入哪个桶
if (!bucket[j]) {
bucket[j] = [];
}
// 通过插入排序将数字插入到桶中的合适位置
s = bucket[j].length;
if (s > 0) {
k = s - 1
while(k >=0){
if (bucket[j][k] > temp) {
bucket[j][k + 1] = bucket[j][k];
} else {
break;
}
k--
}
bucket[j][k + 1] = temp;
} else {
bucket[j].push(temp);
}
}
j++
}
i++
}
i = 0
while(i < bucketCount){// 循环取出桶中数据
if (bucket[i]) {
k = bucket[i].length;
for (j = 0; j < k; j++) {
result.push(bucket[i][j]);
}
}
i++
}
return result;
}
总结
- 冒泡排序,选择排序,插扑克排序统称为比较排序,极限 最快的时比较排序时间复杂度是NLogN(N×2的对数)。
- 计数排序缺点
- 必须有个hash做个计数工具,
- 计数排序无法对小数和负数排序。
- 桶排序,一个桶放一个范围的数字,在桶里做比较排序,计数排序浪费桶,不用做二次排序;
- 基数排序:10的倍数,个位十位百位千位依次排序,可以适应特别大的数字,桶的个数是固定的,拍数次数看最大数的位数。
- 排序要么浪费空间,要么浪费时间,只能选择一个做优化
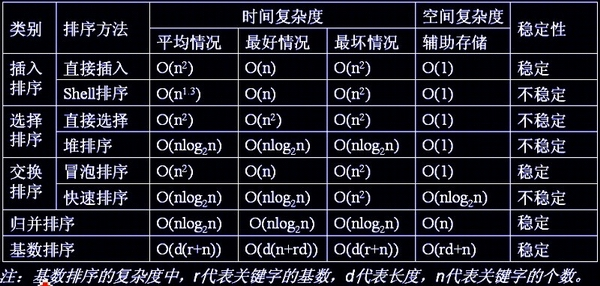
数据结构
- 哈希表(Hash Table)
哈希表就是key:value的组合.1
2
3
4
5
6
7a<- {
'0':0,
'1':1,
'2':2,
'key':'value',
'键':'值'
}
所有满足’键‘:’值’:结构的就是hash(哈希).
数组也是hash,不是数据结构
- 队列(Queue)
先进先出
可以用数组实现
所有与站队相关的模型都应该用队列这种先进先出的模式,a.push a.shift 基数排序也用到队列 - 栈(Stack)
先进后出
可以用数组实现
举例:盗梦空间 stack.push stack.pop - 链表(Linked List)
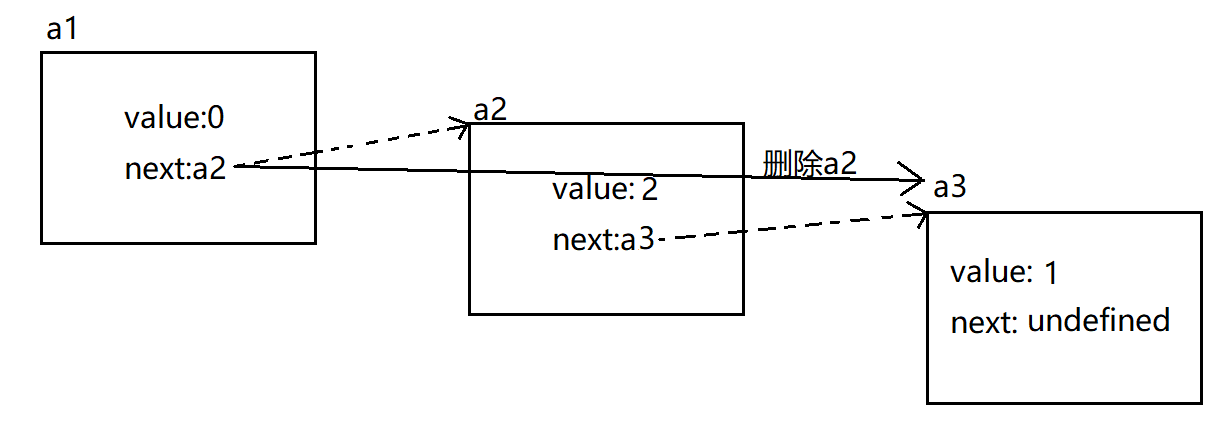
链表是动态的数组,数组查询第n项很快,链表删除比较快,不经常删除或删除头尾使用数组,经常删除中间的用链表
用哈希(JS里面用对象表示哈希)实现链表
head第一个hash对象(链表的表头),其他的叫做node节点,表头也是node - 树(tree)
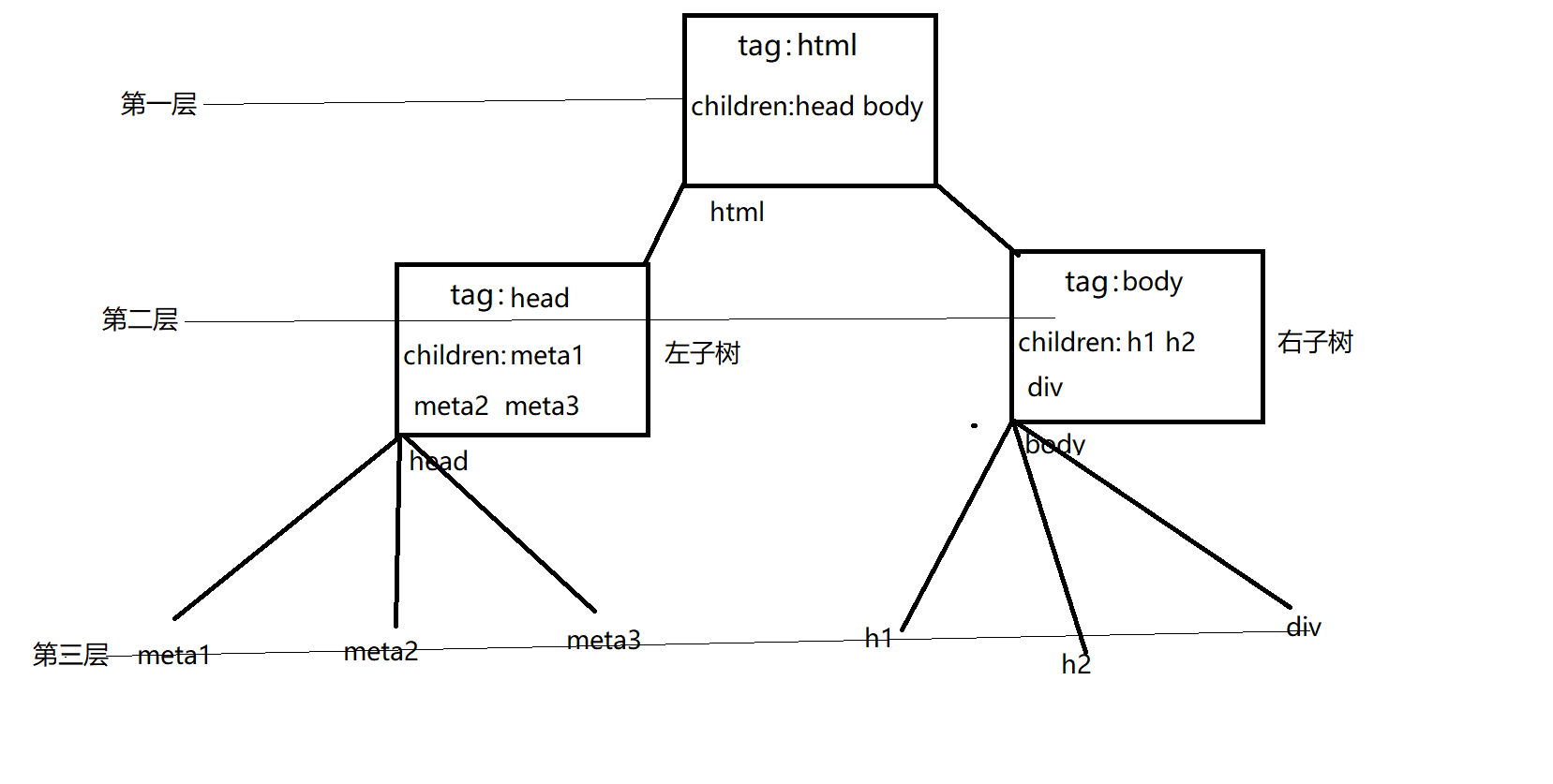
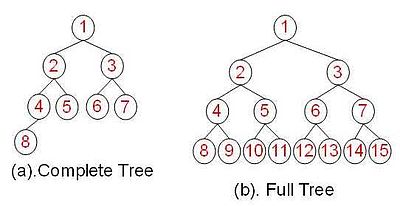
只要用到层级结构就要用到树,满足这种结构的叫做树
不分叉的是链表,分叉的是树,深度是一共有多少层,每个hash就是一个节点,没有子节点的叫叶子节点
二叉树,每次最多分两个叉,从0层开始,第i层最多有2^i节点,最多总共有(2^(i+1))-1个节点
有(2^(i+1))-1个节点的树叫满二叉树,特点是每个层数的节点数都是最大节点数
除了最后一层,其余层节点数都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干加点(一般都是从左往右写的),称为完全二叉树;
完全二叉树和满二叉树可以用数组实现:完全二叉树和满二叉树:a[1, 2,3, 4,5,6,7, 8,9,10,11,12,13,14,15]
如果要取第i层的第k个数字(从第0层开始) a[(2^i-1)-1]+k-1
其他树可以用哈希(对象)实现
操作:增删改查 - 堆
所有子节点的数字都小于父节点的数字的特殊的树叫做堆
- 堆排序用到了 tree,把堆变成最大堆的过程叫做最大堆调整,堆排序就是做最大堆调整,子节点先做对比,大的和父节点做对比
- 堆排序可视化
- 堆排序JS代码完整讲解

Comments